Un autre enseignement des maths en primaire

Stella Baruk : Expérimentations et convictions

Il va bientôt y avoir une vingtaine d’années, il me fut proposé de participer à un colloque organisé dans l’île de Rhodes ; colloque qui avait pour sujet les “assistances de tous ordres” destinées à “remédier” aux échecs en mathématiques . Initiative courageuse à l’époque puisque abordant de front des pratiques plus ou moins volontairement ignorées jusqu’alors. Les qualifiant de “problématique mondiale” – ce qui voulait dire caractéristique des pays développés –, il s’agissait des “leçons particulières”, des “maths-secours” et autres “maths-assistance” , destinés à pallier les insuffisances institutionnelles et dont on ne pouvait plus ignorer la prolifération. Ce qui ne pouvait que mettre en évidence l’inégalité flagrante dans le “soutien” que pouvaient ou non apporter, selon les moyens dont ils disposaient, des parents à leurs enfants . Évidence qui ferait naître l’idée sans doute sincèrement généreuse que “l’école doit être son propre recours”, c’est-à-dire apporter à tous le soutien que seuls les riches pouvaient offrir à leurs enfants ; mais en réalité, disposition qui constituait une énième fuite en avant, une énième façon d’éviter les raisons pour lesquelles il fallait un recours.

Invitée comme auteur de Échec et Maths, et “spécialiste” de “remédiations en entretiens particuliers”, il y avait quelque temps déjà que j’étais parvenue, me semblait-il, à comprendre l’essentiel des raisons faisant que, bien évidemment sans le vouloir, l’institution fabriquait elle-même l’“élève en difficulté”. On me disait après Échec et Maths : « Tout ça est bien beau, mais on ne peut pas mettre un précepteur derrière chaque élève qui ne comprend pas ». Or le sens des analyses particulières que je proposais n’était en aucune façon le recours au préceptorat , mais consistait plutôt, à partir de leur accumulation, à tenter d’en dégager des invariants, afin d’en faire bénéficier l’entité naturelle qu’est une classe. Et alors qu’allaient progressivement apparaître des slogans tels que « l’aide à l’élève, c’est-à-dire le cours particulier ou en petit groupe pour les élèves en difficulté, c’est la base de la démocratie », repoussant à plus tard ou jamais l’analyse des difficultés de l’école, il était assez paradoxal pour moi de constater que le travail de l’institution allait exactement en sens inverse du mien.

Pour la majorité des intervenants du colloque de Rhodes il semblait qu’il y avait lieu de s’accommoder d’un état de fait, un fait dit de société , alors que pour ma part, il me paraissait qu’un « fait de société » tel que celui-là n’était jamais que le résultat de l’acceptation des conditions qui l’imposent : que donc, reconsidérer parmi ces conditions celles sur lesquelles on peut intervenir peut transformer cet état de fait. La masse étant une entité discrète, c’est-à-dire constituée par du un, plus un, plus un, on peut comprendre quel peut être l’intérêt d’avoir travaillé avec des individualités ; mais pour en faire bénéficier le groupe. Mon intervention à Rhodes s’intitulait donc : Comment passer du particulier au général et se trouvait être contemporaine d’une première “expérimentation” de cette conviction, dans deux écoles de l’avenue de la République à Paris.

Il ne m’avait jamais paru acceptable que certains enfants au bout de deux mois de CP soient déclarés “en difficulté”. Je me souviens comment un jour, exaspérée par l’impuissance d’une enfant, impuissance dans laquelle elle n’aurait jamais dû être, et recevant juste après un coup de fil d’une inspectrice me demandant d’intervenir devant des enseignants de l’Enseignement spécialisé, je l’apostrophai, alors qu’elle n’y était pour rien : « Mais pourquoi me demande-t-on, sans cesse, de parler devant des rééducateurs ? Pour que les choses changent, c’est d’abord aux éducateurs qu’il faudrait s’adresser ! »

M’ayant entendue exprimer plus calmement mais avec toujours autant de conviction la même revendication devant des enseignants, encore, spécialisés, c’est une autre inspectrice Madame Jeanne-Marie Tisseyre, à laquelle je rends grâce ici une fois de plus, qui allait intervenir de façon décisive dans le tour que prenaient mes recherches. « Pourquoi avais-je demandé, faut-il “réparer” des élèves alors qu’il suffirait de ne pas les abîmer ? » Très vite, en effet, d’un côté la souffrance et les larmes rendaient l’enfant mutique, ou apathique, ou violent, et de l’autre les “réparateurs” trouvaient une situation rendue d’autant plus difficile que s’y ajoutaient les pressions de l’appareil institutionnel et les angoisses du milieu familial ; le tout pour de trop nombreux cas où le “handicap” de l’élève n’était autre que celui de l’impossibilité où il était de trouver par lui-même ou à ses côtés choses ou gens susceptibles de rétablir le sens qu’il ne trouvait pas à l’école , et que ne lui apporterait aucun soutien ne faisant que reproduire ce qu’on lui avait déjà proposé.

Les mathématiques étant encore plus naturellement “verticales” que toute autre discipline, l’idée que j’avais déjà eue plusieurs années plus tôt était de proposer un suivi d’une cohorte d’enfants du CP au CM2 munis de ce dont je les croyais capables en mathématiques. J’avais la conviction que le taux d’échec serait incomparablement amoindri, l’abord du collège transformé. L’ambition n’était pas mince. Ce projet une fois soumis à Madame Tisseyre, celle-ci me proposa sa circonscription pour une expérimentation : deux écoles, Avenue de la République à Paris, l’une en ZEP et l’autre non. Des enseignants seraient volontaires dans les deux écoles, il n’y avait plus qu’à commencer.

Enthousiaste, je donnai mon accord ; nous commençâmes donc en septembre 1993. Tout était à faire, sinon à inventer. Mettre en forme un apprentissage de la numération, des opérations, des calculs, des problèmes, de la géométrie, à mains nues. Une chance remarquable s’offrit alors. Alors que je l’avais rencontrée pour un tout autre sujet, Isabelle Magnard s’intéressa à l’expérience. Deux années durant, à partir des pages que je préparais pour nourrir au jour le jour les deux classes de CP puis de CE1 de ces mathématiques “différemment” abordées, les Éditions Magnard fournirent les documents en couleur qui rendaient la vie quotidienne de la classe paisible et “naturelle”, sinon celle de qui fut chargée de la fabrication de ces documents expérimentaux et de la mienne. C’est bien naturellement qu’ils apparaissent dans le “récit” de ces expérimentations, matière rendue “éternellement” vivante de la façon dont Julie, Jean-Mathieu, Dahdjim, Justine, Anaïs et les autres vécurent cet apprentissage de mathématiques fondées sur la langue et le sens.

De 1998 à 2000, une autre expérience fut menée dans deux écoles du 14ème arrondissement, sous la houlette, cette fois de l’INRP, toujours en CP puis CE1 . Elle ne fit que confirmer les résultats de la première. Pratiquement plus d’échecs en numération, un calcul mental et écrit qui coulait de source… Et les problèmes… Et la géométrie… Dans les deux expériences, je venais dans les classes une fois par semaine, “initiant” un nouveau sujet, retrouvant dans les résultats des enfants scrutés de près, analysés, le formidable travail des enseignants. La cohérence de “la méthode” fondée sur la langue et le sens, et, évidemment, les mathématiques, leur apparaissait au fur et à mesure que s’avançait l’année. De quoi étaient donc capables des petits CP en fin d’année ? De lire – voire d’écrire - des millions, de faire des problèmes en ayant à choisir une opération, d’expliquer leurs démarches… En fin de CE1 on avait une numération solide, des problèmes complexes dont il fallait trouver les opérations intermédiaires… Mais en tous cas, des enfants jamais angoissés, jamais soumis à un jugement, les erreurs étant discutées en classe, les consensus obtenus sur, précisément, le sens de ce qui était demandé, et celui des réponses que ces questions induisaient, produisaient…

Deux volumes intitulés Comptes pour petits et grands rendent compte de ces expériences : le premier paru en 1997 était consacré à la numération, socle de tout socle commun, et en 2003 le second, consacré aux opérations et calculs.

Miracle des livres : ils circulent, propagent des idées, lesquelles apportent parfois des éléments de réflexion à des questions restées jusqu’alors sans réponse, suscitent des désirs d’innover, d’essayer… Leur vocation de “bouteille à la mer” leur fit aborder les rivages de la lointaine Nouvelle Calédonie, dont le gouvernement , sous l’égide de la direction de l’enseignement, me confia au cours de quatre lumineux séjours (2000-2003) un passionnant travail qui me menait partout, sur le caillou, en brousse comme dans les quartiers les plus déshérités de Nouméa, constater les difficultés qu’affrontaient les maîtres. Partager avec eux, dans une atmosphère rendue féconde par la nouveauté, les discussions, les propositions venant de tous, la recherche de moyens différents de transmettre les bases de l’écriture et du sens des nombres, ou du dessin et des propriétés des figures fut une expérience particulièrement riche et chaleureuse.

On trouvera dans Comptes pour petits et grands le détail des expérimentations parisiennes, un compte rendu sur le site de l’INRP déjà mentionné ; on pourra lire un reportage dans une école de la région parisienne dans le Monde 2, du 13 septembre 2008 ; consulter un dossier-bilan de l’expérience calédonienne. Plus proches, et, cette fois-ci, sans nulle intervention de ma part, nombre d’enseignants de l’Hexagone, désespérant jusqu’alors de combler l’écart entre le travail fourni et les résultats obtenus, me disent avoir tenté puis adopté partie ou tout des méthodes que je propose, ou en font état sur la toile. Voici par exemple un témoignage “à chaud” de Rodolphe Viardet, professeur des écoles, maître formateur, qui me touche particulièrement car les enfants sont en pleine “expérimentation” de la totalité de ce que je propose, dans les domaines tant numérique que géométrique où il y a aussi tant à faire :

J’enseigne au C. P. depuis 5 ans à l’école Henri Wallon A de Bagneux 92. L’école est classée en Réseau d’Education Prioritaire. J’ai tout d’abord essayé d’enseigner avec des manuels traditionnels dédiés au C.P Les enfants comptaient beaucoup et de tout, ils groupaient des allumettes et « construisaient » la dizaine, ils comptaient loin, très loin, ils échangeaient des pièces contre des billets, ils se déplaçaient sur des bandes numériques en « avant » ou en « arrière »… mais je ne me suis rapidement rendu compte que j’avais des difficultés à donner du sens aux exercices proposés…

Après avoir découvert Stella Baruk et la cohérence de son travail, mes élèves et moi-même avons enfin commencé à parler la même langue : celles des mathématiques qui nous parle si souvent et que Stella nous apprend à entendre. Finalement tout devient si simple pour eux et pour moi. En numération, on commence doucement, jusqu’à neuf… Et puis tout est là pour nous guider ! Les doigts, les mots, les chiffres qui n’arrêtent pas de se mêler ; à chaque séance de nouveaux nombres font leur apparition : les cachottiers, les nombre rigolos, les vingts (parfois ils sont quatre)…

Mais attention, tout n’est pas toujours rose, certains chiffres “mentent” alors que d’autres “disent la vérité”… Mais en fin de compte, cependant « mes C.P » sont rassurés car à chaque fois tout s’éclaircit.
Lorsque je demande aux élèves d’écrire un nombre ou de le représenter, ils demandent toujours : en mots ? en chiffres ? avec des étiquettes ?

Jamais une séance sans découverte ni outils (des étiquettes/doigts, des doubles, les mains des camarades…) et les problèmes de la classe deviennent ceux de chacun… Mes élèves demandent toujours : « quand ça commence les maths ? »

“Quand ça commence les maths ?” Eh bien, tout de suite. L’essentiel de ce que je propose semblerait se limiter à une vérité de La Palice. Faire en sorte que dès le CP ce que les enfants apprennent en mathématiques, discipline supposée être le comble du sens – souvenez-vous, rien ne saurait être aussi sûr que 2 et 2 font quatre – ait du sens pour eux, comme pour ceux qui les leur enseignent. Or voici quarante années bientôt que j’observe, avec d’autres acteurs du monde enseignant, les mêmes “incroyables” conduites de la part d’enfants sensés, s’agissant de “donner” l’âge du capitaine, ou d’écrire que « trois cent quatre-vingt-sept » s’écrit 3004207. En quelques mois d’école, les enfants renoncent au sens, l’abandonnant à leurs enseignants, souhaitant qu’ils trouvent dans les réponses qu’ils feront à des questions devenues incompréhensibles ce qu’ils souhaitent. Aliénation qui m’a toujours paru inconcevable, sachant les dégâts provoqués, sans commune mesure avec les causes, qu’il suffit de reconsidérer.

Reconsidérer la matière, en reconsidérant la façon de travailler, c’est-à-dire la manière : l’erreur, dont je n’arrive même plus à penser qu’elle est une erreur quand elle est “fraîche”, tant elle est l’auxiliaire la plus sûre de qui enseigne, à qui elle renverra les ambiguïtés de la langue utilisée, les imprécisions d’une formulation, les interrogations sur les “objets” du savoir. Quand un enfant non encore paralysé par la crainte de se tromper répond, il répond avec ce qu’il sait, et non avec ce qu’il ne sait pas. Si cette réponse n’est pas conforme à ce qui est attendu, elle devient question : pourquoi ? Pourquoi ce que je crois être la réponse à la question posée n’est pas vrai ? Analyser les raisons des erreurs fraîches, en constater la “légitimité”, leur faire une place à côté de la “vérité » à laquelle on souhaite accéder, telle est cette pédagogie qui mène à l’épistémologie, constant questionnement sur la nature et la forme du savoir proposé ; et qui est combien féconde à quelque niveau que ce soit.

C’est ainsi que tout le domaine du savoir à transmettre « de la maternelle à l’université » s’est trouvé pour moi refondé, matière et manière, soutenu par une problématique de sens, de langue, de spécificité du savoir mathématique.

Il n’est guère possible d’en donner ici un “panorama”, même en se limitant à l’école. Je sais cependant que nombre de ceux qui expérimentent ce que je propose sont particulièrement convaincus par un abord de la numération fondé sur la langue et le sens.

La numération, constitutive de tout le domaine du numérique, nécessairement imposée de façon précoce, est cause de beaucoup d’échecs, car elle est difficile. Or c’est d’elle dont dépend le capital numérique à venir des élèves. Comment se pense, s’écrit un nombre ? Quelles sont les relations entre le lu, le su, le vu et l’entendu ? Comment, à partir de ce bricolage qu’est notre langue numérale arriver à construire un système “implacablement” cohérent (le système décimal) ? Sans aucun doute avec la langue, car c’est à partir de cette matière première que les enfants entendent ce qu’ils entendent et comprennent ce qu’ils comprennent. L’ignorer, ou la considérer comme le veut la tradition comme un simple “vocabulaire”, c’est travailler contre elle, et tuer le sens.

Enseignement du nombre fondé sur la langue du nombre, qui permettra à quiconque entre à l’école d’y apprendre le maniement tant mathématique que quantitatif, c’est-à-dire socialisé, du nombre… C’est ce qui, je crois, s’est constitué à travers le temps par une lutte constante contre l’échec, un travail constant avec les enseignants. C’est pourquoi nul ne pouvait mieux en rendre compte qu’un “expérimentateur”, et ce alors que quelques années de pratique lui ont permis de s’approprier et de faire sienne une démarche qui sans doute correspondait déjà à un questionnement ; questionnement qui en particulier pour nombre de professeurs des écoles que j’ai rencontré naît, alors que le travail qu’ils fournissent est considérable, de leur relative impuissance à surmonter les échecs des enfants ; le tout comme si ils s’apercevaient que c’étaient les moyens fournis par la tradition pédagogique qui montraient leur impuissance.

On trouvera donc, comme point fort de ce que je peux proposer pour que notre école primaire devienne une école première, exposé mieux que je ne saurais le faire, le compte rendu qu’en a fait Guillaume Tremblay, professeur des écoles, enseignant en CP, que je remercie chaleureusement ici.

Guillaume Tremblay : La méthode Baruk ou comment donner du sens aux nombres en s’appuyant sur les ressources de la langue

Les nombres appartiennent à l’univers langagier quotidien des élèves qui les entendent et les disent avant d’apprendre à les lire et les écrire de manière méthodique à l’école. Ils font partie du langage ordinaire que les enfants s’approprient dès qu’ils sont en âge de parler. Leur apprentissage en tant qu’objets de la langue non seulement commune mais aussi mathématique est en revanche une spécificité de l’école. Il est d’autant plus crucial pour les élèves de cycle 2 qu’il conditionne ensuite grandement leur réussite tant en numération qu’en calcul. On perçoit bien l’enjeu démocratique de cette entrée en mathématiques.

Or pour être solide, l’apprentissage des nombres doit indissociablement être réflexif et donner accès au sens complexe dont la langue des nombres est porteuse. C’est la démarche que Stella Baruk défend dans Comptes pour petits et grands (volume 1, Magnard, 2003, [CPPG1]), un outil pédagogique issu d’une expérimentation dans des classes de CP/CE1. Nous nous efforcerons ici d’en présenter la logique, en abordant d’un point de vue pratique la conduite des premiers apprentissages numériques à l’école élémentaire, dont l’importance pour la suite de la scolarité vient d’être soulignée.

Nous reviendrons dans un premier temps sur la nécessité pour les élèves de maîtriser la langue des nombres dans sa multiplicité, en distinguant bien ce qui relève de l’usage courant du quantitatif et ce qui renvoie au sens mathématique et à la double écriture du nombre, en chiffres et en mots. Cette double écriture, ainsi que les différentes représentations possibles du nombre, seront fondamentales dans l’approche des nombres inférieurs à 10 que nous détaillerons dans un second temps. Nous aborderons enfin l’écriture et la lecture des nombres à deux chiffres, en expliquant pourquoi la méthode Baruk préconise de commencer par le nombre 37 et non par 10…

La langue des nombres : usage courant et sens mathématique

Sortir de l’opacité numérique

Les nombres tout d’abord se parlent. Un enfant entend et parle avant d’écrire. Comme pour tout objet de pensée, le mode premier d’expression des nombres est celui des mots. La parole première de l’enfant, son écoute de la parole des autres, ont l’avantage de véhiculer du sens, et l’inconvénient de ne suivre aucun ordre particulier dans la capitalisation qui s’en fait au fur et à mesure que l’enfant grandit. La langue des nombres subit le même sort.

Les enfants sont immergés dans un monde saturé de signes dont ceux de la langue des nombres, particulièrement dans une société qui privilégie l’information chiffrée, quantifiée. Permettre aux enfants de lire-écrire la langue des nombres, c’est donc non seulement les ouvrir sur le savoir mathématique mais aussi les ouvrir au monde, et ne pas les laisser se débattre dans ce que Stella Baruk appelle « l’opacité numérique ».

Mais il s’agira pour y parvenir d’établir une distinction entre le savoir socialisé de la quantité et un savoir mathématique du nombre. Ces deux aspects essentiels et dissymétriques doivent coexister pacifiquement. La prise en compte d’habitudes quantitatives particulières, leur nécessaire distinction d’avec l’« universalité » mathématique sont essentielles à l’élaboration du sens. Inversement, le mélange qui se fait traditionnellement du quantitatif et du mathématique est à l’origine de bien des confusions dans les apprentissages mathématiques.

Nombres et « nombres-de »

La double fonction de la numération, fonction de lecture courante du monde qui nous entoure, et fonction « savante » de savoir mathématique, renvoie à deux notions que Stella Baruk nous invite à distinguer, les « nombres-de » et les nombres.

Les « nombres-de » rendent compte de quantités. Nous appellerons ainsi les nombres suivis de ce qu’ils comptent, évaluent ou mesurent. Ces expressions rendent compte de quantités, elles peuvent s’adresser directement à l’enfant (« un lapin a quatre pattes ») mais il peut aussi les entendre sans que cela lui soit adressé (cf. les milliards prêtés aux banques…). Dans la phrase « un lapin a quatre pattes », « quatre » dit le nombre-de pattes du lapin. C’est un nombre-de.

Le nombre est une idée qui permet de se représenter la quantité. On peut dire « quatre » tout seul. « Quatre » tout seul n’est pas un nombre-de. Ce n’est pas une quantité, c’est un nombre, c’est-à-dire une idée, qui permet à l’imagination de marcher, de se représenter une quantité.

Langue numérale et langue numérique, la double écriture du nombre

Les nombres ont ceci de singulier dans la langue qu’ils s’écrivent d’une part en mots et d’autre part en chiffres. Le nombre « quatre » peut se dire et s’écrire en mot, mais il a aussi une autre écriture, en chiffre : 4. Les nombres sont en effet les seuls mots de la langue à avoir deux écritures. Avec Stella Baruk, nous désignerons par « langue numérale » tous les mots qui mettent en jeu des nombres et par « langue numérique », la traduction chiffrée de ces expressions numérales. En numéral, les nombres s’écrivent en mots. En numérique, ils s’écrivent en chiffres.

Les chiffres sont des signes qui proposent une seconde écriture pour transcrire un mot qui a déjà son écriture propre. Il s’agit de signes étrangers à ceux qui permettent d’écrire une langue. L’écriture chiffrée usuelle utilise les dix chiffres : 1,2, 3, 4, 5, 6, 7, 8, 9, 0. Une fois un système de numération choisi, les nombres n’ont qu’une seule écriture chiffrée.

Notons la difficulté liée au fait que la langue commune utilise couramment « chiffre » en lieu et place de « nombre ». La langue commune est comme elle est mais la distinction à faire en classe, et en mathématiques, entre nombres et chiffres est essentielle.

Voyons maintenant comment se décline le travail avec les élèves de cycle2 sur les nombres-de, les nombres et leur double écriture, tout d’abord sur les nombres inférieurs à dix.

Avant dix

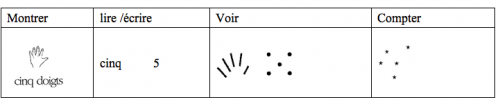
Le travail proprement dit de lecture-écriture et son enracinement dans du sens va se faire d’abord sur « cinq », puis autour. Pour qu’il y ait « sentiment de nombre », il faut qu’il y ait du nombreux, c’est pourquoi on prendra « cinq » pour « pivot ». Seront ensuite abordés « six » et « sept », puis « quatre » et « trois », et enfin les extrêmes : « huit » et « neuf », puis « deux » et « un ».

A ce niveau, le matériau langagier convoqué sera la comptine numérique déjà connue et imprimant un ordre. On aura également recours aux comptines spécifiques qui incluent certains mots numéraux parmi d’autres (comme par exemple « voici ma main elle a cinq doigts… »).

Donner le sentiment du nombre à l’aide de représentations variées

Nombres et nombres-de sont susceptibles de représentations qu’on donnera à voir aux élèves. Pour donner le « sentiment » du nombre aux enfants, on leur présentera, en les distinguant, des représentations matérialisées de nombres-de et des représentations idéalisées du nombre. Les représentations matérialisées de nombres-de auront pour support des objets quelconques (billes, pommes…) ou les doigts de la main. Tandis que pour les représentations idéalisées, nous utiliserons des entités désincarnées, points ou barres, notamment des doigts sous forme de barres, ayant l’avantage de préserver le statut d’idéalité du nombre.

On insistera tout particulièrement sur le matériel privilégié que constituent les doigts, aussi bien « en vrai », incarnations de nombres-de, qu’en représentations idéalisées. De toutes les perceptions possibles de nombres-de, celles des doigts offrent un avantage indiscutable. On commencera donc par là. La morphologie et le nombre de doigts sont fondamentaux. Bien sûr les nombres-de doigts sont des nombres-de, mais comme nous le verrons plus tard avec les nombres à deux chiffres, les doigts permettent un accès privilégié au sens de l’écriture chiffrée qui est ce qu’elle est, une écriture décimale, autrement dit une écriture en base « dix », parce que nous avons dix doigts. Nous appellerons « monstration » l’action destinée à évoquer un nombre en montrant un nombre-de doigts. Quant aux représentations idéalisées du nombre, les doigts sous forme de barres permettront la reconnaissance immédiate des nombres représentés.

2.2 Le sens des nombres-de

Concernant les représentations matérialisées, on réfléchira sur le sens (ou l’absence de sens) du dénombrement d’objets. Il s’agit de porter un regard mathématique sur des objets non mathématiques. On peut compter ensemble des poires, mais si elles sont de différentes tailles, ou mélangées avec d’autres fruits, le dénombrement a-t-il toujours du sens ? Pour pouvoir dire un nombre-de, il faut qu’existe un mot qui permet de « parler le nombre », un terme transitif qui homogénéise la collection. On peut sans doute compter ensemble des pommes et des poires car il s’agit de fruits, par contre compter ensemble des poires et des stylos n’a aucun sens, il n’y pas de terme transitif permettant de les réunir. Les enfants s’amusent beaucoup à proposer ou refuser l’existence de termes transitifs justifiant l’existence d’un nombre-de.

L’organisation de la représentation idéalisée

Pour ce qui est des représentations idéalisées en points ou en barres, on insistera sur l’organisation permettant la reconnaissance immédiate ou rapide. On mettra en évidence les différentes perceptions que propose une représentation visuelle des nombres inférieurs à dix, selon que cette représentation est organisée ou non (sachant qu’en français la parole n’organise le nombre qu’après dix) : non organisée, il faut compter pour savoir « combien il y a », dénombrer ; organisée, « on voit tout de suite combien il y a », on peut tout de suite « nombrer ».

La disposition idéalisée des doigts sous forme de barres aura pour nous une importance particulière : elle est immédiatement reconnaissable pour les enfants. Nous apprendrons également les dispositions géométriques qui permettent la perception instantanée des nombres avant dix, par exemple « cinq » sous forme de pentagone.

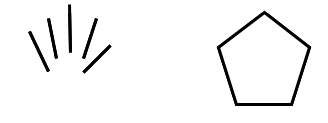
Maîtriser la double écriture des nombres

Des exercices seront proposés pour reconnaître et savoir écrire les nombres avant « dix » en chiffre et en mot. Notons que l’écriture chiffrée fournit aux mots numéraux une garantie que n’ont pas les autres mots de la langue. On peut par ailleurs constater avec les enfants que les mots pour dire les nombres dans chaque langue sont différents alors que leur écriture chiffrée est la même.

L’objectif final est que convergent toutes les composantes qui donneront leur assise solide aux nombres précédant dix : la coïncidence du dénombrement (ordinal) et du « nombrement » (cardinal), et celle de l’écriture numérale et numérique. Les enfants sont ainsi supposés faire connaissance des nombres de un à neuf. Ces nombres sont en effet explorés pour eux-mêmes et les diverses incarnations de chacun doivent être bien présentes. « Huit » par exemple doit : évoquer un mot parlé , être matérialisable en nombre-de , représentable en nombre ; on peut l’écrire en mot, mais aussi en chiffre ; il a sa place dans la suite des nombres.

La correspondance du numéral avec le numérique a une importance particulière. Elle doit être solidement établie. Sans cela, les écritures comportant deux chiffres seront opaques, ou muettes, n’évoquant rien dans l’entendement de l’enfant. De même on soulignera l’importance d’initier les enfants à la notion d’organisation : quand le nombre ne s’écrit qu’avec un seul chiffre et ne se dit qu’avec un seul mot, son organisation est « libre » ; au-delà, il faut composer avec la double organisation que supposent la langue et l’écriture chiffrée.

Lire-écrire des nombres à deux chiffres

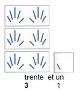
Avec les nombres à deux chiffres se posent les questions que met en jeu un système de numération, autrement dit l’organisation systématique d’une quantité établie de « uns ». Le processus historique fort complexe qui mena à l’écriture des nombres a consisté à fixer la quantité représentée de manière à la rendre aisément perceptible, ce qui suppose de l’organiser. Dans notre système de numération, les nombres sont organisés en base dix parce qu’historiquement on a appris à garder le souvenir des quantités avec les doigts. Jusqu’à neuf, les doigts suffisent à représenter les nombres qui sont des « uns » mis côte à côte. Après, les nombres sont organisés par « paquets » de dix : les dix doigts pris ensemble vont constituer une nouvelle unité. Pour initier les élèves à ce système complexe d’organisation, Stella Baruk propose de s’appuyer, outre le recours aux doigts, sur les ressources qu’offre la langue en faisant notamment entendre aux élèves le principe d’organisation qui la structure. C’est pourquoi nous commencerons par le nombre 37 : le « trente » de « trente-sept », dans lequel on entend bien le « tr » de trois, veut dire trois paquets de dix et s’écrit en effet avec le chiffre 3. Il y a une correspondance à ce niveau entre ce qui se dit dans la langue numérale, ce qui s’écrit dans la langue numérique, et ce qu’on peut représenter avec les doigts. L’accès au sens de l’écriture chiffrée dans notre système de numération est ainsi plus aisé avec 37 qu’avec 11 ! Voyons maintenant, en entrant dans le détail de la pratique de classe, comment s’articulent ces principes avec une progression qui permet un apprentissage efficace des nombres à deux chiffres.

Entendre, dire et écrire les nombres à deux chiffres, de 30 à 69

La langue numérale, qui se parle et s’entend, répond à un principe d’organisation. On s’appuiera donc sur elle pour aborder les nombres à deux chiffres et le système de numération. L’écriture seconde du nombre, la numérique, ne fait que « doubler » la parole, qui est chargée de significations et d’informations qu’on s’attachera à rendre explicites. Il faut donner du sens au nombre qui se dit, permettre à l’enfant de reconnaître dans ce qu’il entend la façon dont s’organise le nombre. On apprendra à lire et à écrire en numéral et en numérique ce qui se dit, afin de rendre cohérentes la parole et sa « double écriture ».

Dire « trente-sept » suppose déjà un groupement en 3 « paquets de dix », lesquels sont ce qu’ils sont parce que nous avons dix doigts. Mais pour que l’entité constituée par dix « uns » apparaisse avec le nouveau visage de un « dix », c’est-à-dire en tant que nouvelle unité, il faut qu’il y en ait plusieurs. D’où le fait de commencer avec les enfants par « trente-sept », nombre qui n’a pas été choisi au hasard : il s’identifie aisément à l’œil et à l’oreille, et les allers-retours entre toutes ses expressions convergent aisément pour donner du sens à ce qui est déjà dans l’entendement. Et comme nous le verrons, il sera précieux pour la suite des évènements…

Notons que le plus difficile de la numération est la « tranche » de dix à cent, à cause principalement de l’écart entre ce qui se dit et ce qui s’écrit pour les nombres entre dix et trente, et ceux après soixante-dix. Difficiles parmi les difficiles sont les nombres de dix à vingt. Cette épreuve est traditionnellement ce qui attend les enfants en premier : avec Stella Baruk, nous ne l’aborderons qu’une fois entraînés à lire-écrire des nombres qui laisseront plus volontiers apparaître du sens, et de la cohérence entre le lu, le su, le vu et l’entendu.

Commençons donc par trente-sept. En classe de CP, on imagine avec les enfants qu’on doit faire savoir à quelqu’un qui nous regarde mais ne peut nous entendre parce qu’il est dans la cour par exemple, qu’il faut trente-sept assiettes pour le goûter. On n’a plus assez de doigts :

  Les deux mains en l’air, nos poings fermés, on lui montre nos dix doigts, une, deux, trois fois, et puis on montre un « sept ».

  On écrit au tableau « trente-sept » en mots. On fait lire aux enfants : le sept est familier, le « tr » du trente peut se déduire du trois, il reste à décoder « ente » et le trait d’union qui fait qu’un seul objet se dit avec deux mots.

  On l’écrit maintenant en chiffres en plaçant sous le « sept » le « 7 » que nous connaissons bien puis sous le « trente », un « 3 », après avoir réécrit les deux premières lettres « tr » en couleurs. Ce « trois » est un trrrois qui veut dire trrrente. On donne bien à entendre le trrr qui permet d’associer « trente » à l’écriture de « 3 ». On explicite en montrant la correspondance mot/chiffre au tableau : trente-sept s’écrit avec un 3 qui vaut trente, et un 7 qui vaut sept, qui « dit la vérité » (« 3 » ne ment pas, mais il dit autre chose que 3 « uns »).

S’ensuit une série d’exercices sur les nombres de « trente et un » à « trente-neuf » : le maître montre, les élèves doivent dire les nombres ; les élèves montrent les nombres demandés ; le maître montre ou écrit en mots au tableau, les élèves écrivent les nombres en chiffres.

Trente-trois sera le premier nombre « rigolo » rencontré, puisqu’il s’écrit avec un « 3 » qui vaut « trente » et un « 3 » qui dit la vérité.

Ensuite on dicte aux enfants les nombres, en faisant d’abord monter la voix et en s’attardant sur le « en » de trente, puis en la laissant retomber : trente, quatre etc. On enchaîne rapidement. Et maintenant, attention : trente… et là, on se met la main sur la bouche, on n’a plus rien à dire. On a besoin d’un signe pour dire qu’on n’a plus rien à dire : ce signe, c’est zéro, « le chiffre du silence », qui est là pour marquer une place vide.

La succession rythmée des gestes pour répéter « dix » va être complétée par une représentation plus stable et rassurante : les « logos » destinés à évoquer le « dix » des dix doigts vont permettre de donner une représentation organisée des nombres, calquée sur son organisation parlée. Les enfants n’auront plus qu’à comptabiliser des « dix » fixés au tableau et reconnaître les « uns » familiers qui les accompagnent.

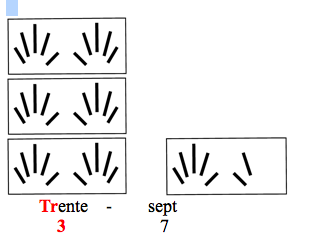
Une fois le processus entamé avec trente, il se poursuit aisément pour les quarante, cinquante et soixante : à partir de trente, un carton de dix supplémentaire au tableau, un geste de plus avec les mains, le qua qui rappelle le quatre, et l’on a quarante et quelque. En gardant le « sept » final très commode, on affichera successivement au tableau quarante-sept, puis cinquante-sept, puis soixante-sept. Dans « cinquante », le « cinq » s’entend dans son intégralité. Après, il faudra être plus attentif : au sifflement du sssoixante qui rappelle celui du sssix et, aux « ente » ou « ante » qui nous « expliquent » que ce qui est compté jusqu’à trois, quatre, cinq ou six, ce sont des paquets de dix.
On reprend les mêmes exercices que pour trente et quelque : dire ou écrire à partir de monstrations avec les mains ou avec les étiquettes, montrer avec les doigts ou les étiquettes des nombres dits ou écrits, écrire sous la dictée des nombres où le second chiffre est celui du silence. Presque tout le complexe de trente à soixante-neuf est en place. Pour le compléter, on portera une attention particulière sur l’écriture des mots « trente », « quarante », cinquante » et « soixante » afin que les enfants puissent écrire en mots les nombres figurés par les cartons. On insistera toujours sur la double écriture, en proposant régulièrement des dictées de nombres à écrire en mots et en chiffres. On mettra aussi en évidence la particularité en mots des « trente et un », « quarante et un », « cinquante et un », « soixante et un ».

Quand les mots ne rendent plus de comptes : la descente sur vingt puis sur dix et la rencontre des cachottiers

Une attention spéciale est accordée à vingt en raison de sa « pauvreté » et du fait qu’on n’entend plus rien de son organisation en deux dizaines. Cette pauvreté dans la matière, et dans l’évocation sonore, suppose que l’on procède par appauvrissement d’une matière riche, et sonore.

Au tableau se trouvent donc les cartons représentant « 67 » : un sssoixante-sept où le « 6 » est évoqué par le sss, et dont le « 7 » qui est bien connu restera là jusqu’au bout. On l’écrit en chiffres dessous. Un carton de « dix » disparaît : cinquante-sept ! On l’écrit, 57, on le redit, et puis ainsi de suite : quarante-sept, 47, trente-sept, 37, et puis on n’a plus que 2 paquets de dix. Ce deux, on ne l’entend plus du tout dans ce qui se dit, « vingt ». Dans « vingt-sept », qui s’écrit en chiffres 27, la correspondance entre ce qui se dit et ce qui s’écrit est rompue au niveau des dizaines, en revanche elle est maintenue au niveau des « uns » : on n’entend rien du deux dans « vingt », mais on entend bien le « sept » qui dit la vérité.

Une fois assurée l’écriture des nombres de vingt à soixante-neuf, on poursuit, en faisant disparaître à nouveau un carton de « dix » à partir de vingt-sept : « dix-sept ». Si rien ne s’entendait du deux/2 dans l’écriture de « vingt/20 », que dire du un/1 de l’écriture de dix/10 , par ailleurs pauvre parmi les pauvres en matière. Il faut toutefois donner à entendre « dix » là où il s’entend ; et comme par hasard, il ne s’entend qu’à partir du « dix-sept » ! On comprend maintenant pourquoi le « sept » est un repère précieux… On finit donc avec un carton dans la colonne des « dix », et toujours notre sept. Il faut écrire ce un en chiffre, et ce sept qui va avec, 17. On fait remarquer que le un ne s’entend pas. On dicte ensuite, montre et demande de montrer « dix-huit » et « dix-neuf ». C’est tout ce dont on dispose pour donner à entendre ce « dix ». On recommence la dictée : dix-huit, dix-sept, dix-neuf, dix… : main sur la bouche. Le chiffre du silence doit venir s’écrire à côté du un qu’on n’entend pas. Et on arrive ainsi à 10.

On arrive maintenant à la partie la plus ardue, les nombres de 11 à 16. Ici, la correspondance est totalement rompue entre ce qui se dit en mots et ce qui s’écrit en chiffres. On dit « dix-sept », « dix-huit », « dix-neuf », mais on ne dit pas « dix-un, dix-deux, dix-trois, dix-quatre, dix-cinq, dix-six, etc. ». Dès lors comment savoir que nos onze, douze, treize, quatorze, quinze, seize s’écrivent 11, 12, 13, 14, 15, 16. Ces nombres cachent bien leur jeu, c’est pourquoi Stella Baruk les appelle les « cachottiers ». En mots ils ont tout du message caché et ce doublement, car onze, douze, treize, quatorze, quinze, seize ne signifient pas « dix-un, dix-deux, dix-trois etc. » mais plutôt « un et dix, deux et dix, trois et dix etc. ». Il y a un renversement après seize. Avec les enfants, il conviendra de « désosser » les cachottiers et de proposer pour ce qui est du sens, des termes transitifs. On expliquera ainsi que dans « dix-sept », « dix-huit », « dix-neuf », si on n’entend rien du « un » qui permet d’écrire « dix » avec un « 1 », du moins le « dix », lui, on l’entend bien. Dans « seize », le « dix » est non seulement caché dans le zzze, mais renvoyé au bout du mot. C’est donc sssei qui évoque sssix, et zzze le dix : donc ce ssseizzze veut dire « six et dix », mais si nous l’énoncions comme il s’écrit en chiffre, nous dirions plutôt « dix-six ». Ce sera donc « dix-six » que nous adopterons comme terme transitif.

Maintenant que tous ces nombres si difficiles du début ont été explorés, on explicite la notion de dizaine et celle de comptage : quand on compte, on dit le nom des nombres que l’on obtient en partant de un/1, et en ajoutant un, encore un, et ainsi de suite ; chaque fois qu’on arrive à un paquet de dix, on a une nouvelle dizaine, on la compte avec les autres dizaines et on dit un nouveau mot, après lequel on recommence… Il est temps maintenant de procéder à une remise en ordre de 1 à 69 et de faire une pause avant la découverte des nombres de 70 à 99.

Après 70, les dizaines cachées

Nous voici face à ces « monstres langagiers » que sont nos « soixante-dix », « quatre-vingts », « quatre-vingt-dix ». Ces irrégularités de la langue numérale, ont au moins le mérite d’attirer notre attention sur les régularités d’un système, celui des ente ou ante, qui correspond à celui de l’écriture numérique. Nous utiliserons donc là aussi des termes transitifs pour aider à donner du sens à ces nombres : « septante » pour soixante-dix, « huitante » pour quatre-vingts, « nonante » pour quatre-vingt-dix.

On pourra ainsi montrer aux élèves qu’en Belgique et en Suisse, on dit « septante », mais qu’en français on compte sans inventer un nouveau mot après soixante-neuf. On dit soixante-dix. L’écriture en chiffres de 78 est facile à partir d’une représentation avec les cartons. Tout le problème va être la façon de le lire et de le dire. « Soixante-dix » et « septante » sont deux organisations différentes du même nombre dans la langue numérale, alors qu’il n’y aura qu’une façon de l’écrire en chiffres. On va illustrer ces deux façons de dire avec les cartons : à l’aide d’accolades, en juxtaposant soixante et dix d’un côté (soixante-dix) et en regroupant les sept « dix » (septante) de l’autre. Mais attention, avec les élèves on dit soixante-dix comme un seul bloc, et huit tout seul : « soixante-dix, huit ». On dicte en parlant en français ou en suisse : 78, 79, 77 et 70.

Pour aborder les « soixante-…ze », on va se servir de l’écriture chiffrée comme tremplin à la façon de parler : 76 devrait se lire soixante-dix-six, mais on ne peut pas laisser dix-six à la suite, on le remplace par seize, et au lieu de dire soixante-dix-six, on dit soixante-seize.

En fait, après soixante, la langue numérale suit un autre principe d’organisation : au lieu de compter par dix, on compte par vingt, ce qu’on va voir avec « quatre-vingts ». En des temps reculés, et dans certains pays, si on voulait garder le souvenir d’une quantité, et que les doigts ne suffisaient pas, on utilisait aussi ceux des pieds, ce qui faisait vingt en tout. C’est pourquoi certains nombres sont organisés en vingtaines : les huit dizaines font ainsi quatre vingtaines, ce qui se dira quatre-vingts. On peut réinventer un comptage par vingt avec les enfants à l’aide des cartons : un vingt, deux vingts (quarante), trois vingts (soixante), puis quatre-vingts. Dans le système en ante, cela devrait logiquement se dire « huitante ». On se servira de ce terme transitif jusqu’à ce que l’association « quatre-vingts »- « huit dix » se fasse facilement. On peut maintenant travailler les nombres de 81 à 89 puis 80 à partir de dictées, en disant bien le quatre-vingts d’un bloc.

En ajoutant un carton de dix à 80, et en plaçant sept à côté, il est très simple d’écrire en chiffres le nombre représenté, 97. En mots, en français, c’est plus difficile… On propose le nonante suisse comme terme transitif ; le nombre représenté et qui a pour écriture chiffrée 97, se dit aisément en Suisse : nonante-sept. Puis on peut expliquer ensuite de la même façon que pour « soixante-dix ». On peut aussi expliciter le comptage en vingtaines dans l’organisation en mots et le comparer au comptage par dix dans l’écriture chiffrée en s’aidant des cartons : on regroupe ces derniers par vingtaines ou on autonomise les dizaines.

Tout le complexe des nombres de 1 à 99 est maîtrisé, et les élèves qui ont ainsi accès au sens de l’écriture chiffrée pourront mettre à profit ces connaissances précieuses lors de l’apprentissage du calcul et des problèmes qui font d’ailleurs l’objet du second volume de Comptes pour petits et grands de Stella Baruk.

Conclusion

Nous avons vu que la question de l’organisation des expressions numérales révèle une sédimentation diversifiée au cours de l’histoire. Face à cette hétérogénéité linguistique, rappelons que la régularité de l’écriture chiffrée est rassurante dès qu’elle est comparée à ce qui se dit, pour s’y accorder, ou s’en séparer. Amener comme y invite Stella Baruk, les enfants à réfléchir sur ces relations complexes entre langue parlée et langue écrite, à comprendre les systèmes qu’elles traduisent et ainsi à maîtriser le sens des nombres dits, entendus, lus et écrits, c’est permettre à tous de poursuivre les apprentissages mathématiques sur des bases solides. C’est aussi permettre à tous de développer des capacités réflexives utiles à la maîtrise de la langue tout court, et au-delà, d’éprouver le plaisir singulier lié à l’activité intellectuelle. Les réflexions de Stella Baruk seront donc utiles à tous ceux qui parient sur l’égalité des intelligences et qui cherchent des dispositifs pédagogiques pratiques mettant en œuvre le principe d’éducabilité universelle.